回帰分析とは？Pythonでの実装から解釈まで実務で使える完全ガイド

データ分析の基本手法「回帰分析」について、理論よりも実践を重視して解説します。

5分で読めて、すぐ試せる内容です：

回帰分析の基本概念と使いどころ
Pythonでの具体的な実装方法
結果をビジネスに活かす解釈のコツ
よくある失敗パターンと回避方法

対象読者：

データ分析を始めたばかりの方
Pythonで予測モデルを作りたい方
分析結果をビジネスに活かしたい実務担当者

前提知識：

Pythonの基本文法
平均・分散など基本的な統計量の理解

回帰分析とは

回帰分析は、ある変数（目的変数）が他の変数（説明変数）によってどう説明できるかを数式で表す統計手法です。

簡単に言えば「XとYの関係を数値化する」方法です。

2つのタイプ

単回帰分析

1つの説明変数で予測する方法。

例：広告費 → 売上
例：勉強時間 → テストの点数

重回帰分析

複数の説明変数で予測する方法（実務ではこちらが主流）。

例：広告費 + 気温 + 曜日 → 売上
例：面積 + 築年数 + 駅距離 → 不動産価格

こんなときに使える

回帰分析が活躍する場面：

1. 予測・需要予測

来月の売上を予測したい
必要な在庫数を算出したい
将来の需要を見積もりたい

2. 要因分析・施策効果測定

どの要因が売上に影響しているか知りたい
広告費の投資対効果を数値化したい
マーケティング施策の効果を測定したい

3. 価格設定

新製品の適正価格を決めたい
不動産の査定価格を算出したい
競合との価格比較をしたい

回帰分析が使える条件：

✅数値で測れる目的変数がある（売上、価格など）
✅過去データが十分にある（最低50件以上）
✅変数間に何らかの関係性がありそう

✎コラム：お客様に寄り添い、納得感のある意思決定を

「売上を予測したい」というご相談に対し、私たちはすぐに計算を始めることはしません。なぜなら、データはあくまで「過去の事実」の断片に過ぎないからです。

回帰分析のモデルを作る前に、まずはお客様と対話し、現場の状況を丁寧に紐解きます。

「なぜその数字が必要なのか？」
「予測した先に、どんなアクションがあるのか？」

統計的な正しさ（合理）だけでなく、現場の実感（情理）を大切にする。この「課題の整理」こそが、ビジネスで本当に使える分析結果を生むための、私たち分析屋の「おもてなし」です。

お客様の一番近くで、納得感のある意思決定をサポートいたします。

Pythonで実装してみる

環境準備

必要なライブラリをインストール：

pip install numpy pandas scikit-learn matplotlib japanize-matplotlib
　

必要なライブラリをインポート：

import numpy as np
import pandas as pd
import japanize_matplotlib
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
　

単回帰分析の例（基礎理解用）

まずは最もシンプルな「広告費と売上」の関係を分析します。

サンプルデータを用意します。

# サンプルデータ作成
np.random.seed(42)
ad_cost = np.random.uniform(10, 100, 100) # 広告費
sales = 50 + 3 * ad_cost + np.random.normal(0, 20, 100) # 売上

# データフレーム化
df = pd.DataFrame({‘広告費’: ad_cost, ‘売上’: sales})
　

サンプルデータを使って、単回帰分析の学習を実行します。

# モデル作成
X = pd.DataFrame(df[[‘広告費’]])
y = df[‘売上’]
model = LinearRegression()
model.fit(X, y)
　

単回帰分析は「広告費」と「売上」の2次元であるため、可視化が容易にできます。

　
# 可視化
intercept = model.intercept_
coef = model.coef_[0]
r2 = model.score(X, y)

# 1. グラフ内に表示するテキストを作成（LaTeX形式を利用）
stats_text = (f”Regression Equation:\nSales = {intercept:.2f}+{coef:.2f}×広告費\n”f”$R^2 = {r2:.3f}$”)

# 2. 可視化
plt.scatter(df[‘広告費’], df[‘売上’], alpha=0.6, label=’実測値’)
plt.plot(df[‘広告費’], model.predict(X), ‘r-‘, linewidth=2, label=’回帰直線’)

# 3. グラフ内にテキストを配置
plt.gca().text(0.05, 0.95, stats_text, transform=plt.gca().transAxes,
fontsize=9, verticalalignment=’top’,
bbox=dict(boxstyle=’round’, facecolor=’white’, alpha=0.8, edgecolor=’gray’))

plt.xlabel(‘広告費（万円）’)
plt.ylabel(‘売上（万円）’)
plt.title(‘単回帰分析の結果’)
plt.legend(loc=’lower right’)
plt.grid(True, linestyle=’–‘, alpha=0.5)

plt.show()
　

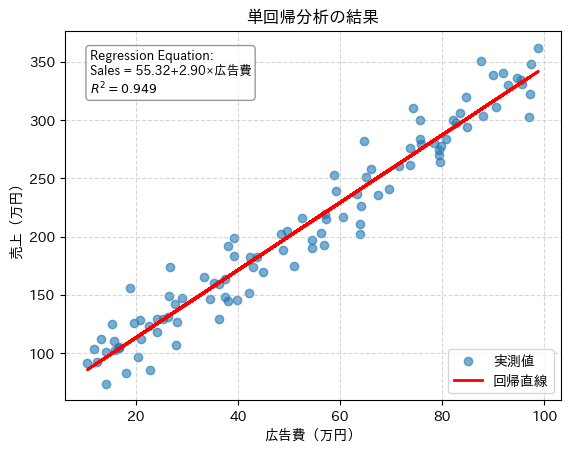
これで単回帰式（Regression Equation）を得ることができました。

単回帰式に当てはめると「広告費を1万円増やすと売上が約3万円増える」ことが分かります。

例えば、広告費を60万円とすると、予測上の売り上げは約229万になります。

重回帰分析の実装（実務向け）

実際のビジネスでは複数の要因を考慮する重回帰分析を使います。

シナリオ：売上を「広告費・気温・週末フラグ」で予測

サンプルデータを新しく作成します。

# サンプルデータ作成（より現実的な設定）
np.random.seed(42)
n = 200

data = {
    ‘広告費’: np.random.uniform(10, 100, n),
    ‘気温’: np.random.uniform(15, 35, n),
    ‘週末’: np.random.binomial(1, 0.3, n) # 0=平日, 1=週末
}

df = pd.DataFrame(data)

# 売上を生成（各要因の影響を設定）
df[‘売上’] = (50 +
              2.5 * df[‘広告費’] +
              3.0 * df[‘気温’] +
              30 * df[‘週末’] +
              np.random.normal(0, 15, n)
　

サンプルデータを使って、重回帰分析の学習を実行します。

# 重回帰モデルの作成
X = df[[‘広告費’, ‘気温’, ‘週末’]]
y = df[‘売上’]

model = LinearRegression()
model.fit(X, y)

# 結果表示
print(“=== 重回帰分析の結果 ===\n”)
print(f”切片: {model.intercept_:.2f}”)
print(“\n各変数の係数:”)
for feature, coef in zip(X.columns, model.coef_):
    print(f” {feature}: {coef:.2f}”)

print(f”\nR² (決定係数): {model.score(X, y):.3f}”)

# 回帰式を表示
print(f”\n回帰式:”)
print(f”売上 = {model.intercept_:.2f} + “
      f”{model.coef_[0]:.2f}×広告費 + “
      f”{model.coef_[1]:.2f}×気温 + “
      f”{model.coef_[2]:.2f}×週末”)
　

以下が出力になります。

=== 重回帰分析の結果 ===

切片: 52.25

各変数の係数:
  広告費: 2.49
  気温: 2.83
  週末: 35.00

R² (決定係数): 0.955

回帰式:
売上 = 52.25 + 2.49×広告費 + 2.83×気温 + 35.00×週末
　

今回の重回帰分析は4次元なので、ギリギリ可視化ができます。

ただ、重回帰分析でこのような可視化をすることは稀なため、ソースコードは省略します。

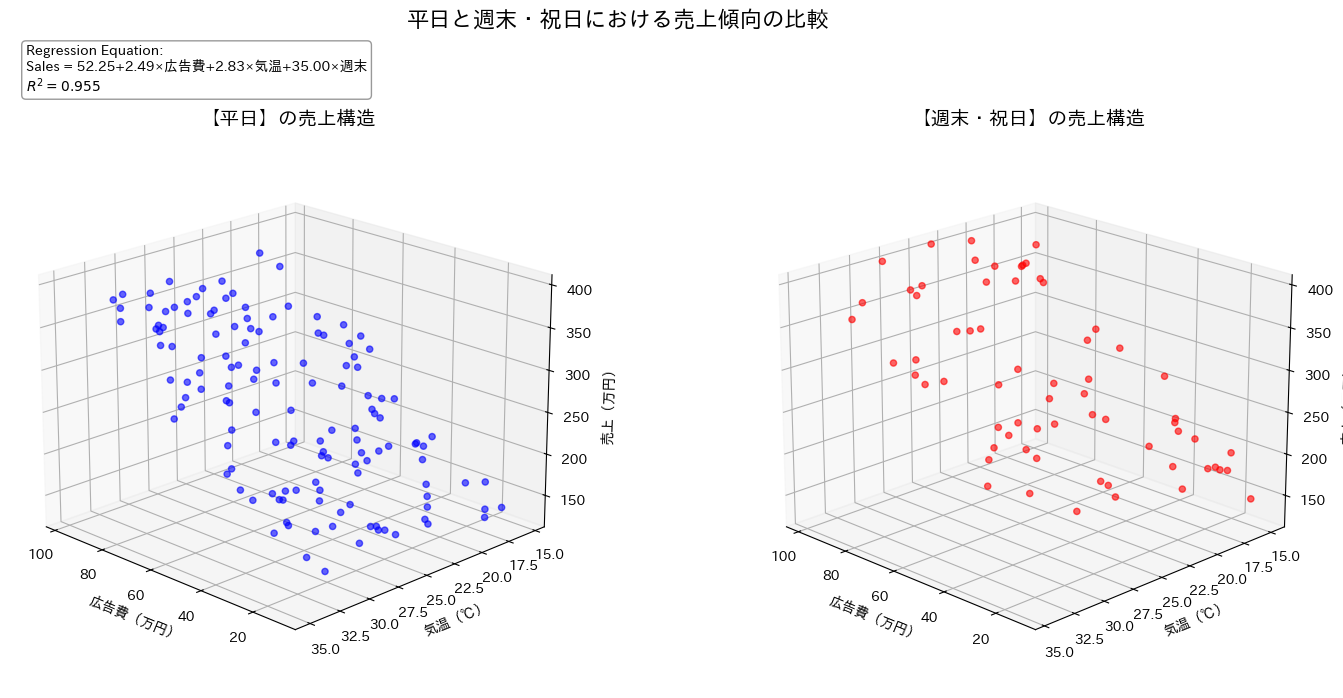
具体的に予測結果を出してみましょう。

# 具体的なシナリオで予測
scenarios = pd.DataFrame({
    ‘広告費’: [50, 80, 50],
    ‘気温’: [25, 25, 30],
    ‘週末’: [0, 0, 1]
})

predictions = model.predict(scenarios)

print(“\n=== 予測シナリオ ===”)
for i, row in scenarios.iterrows():
    print(f”\nシナリオ{i+1}:”)
    print(f” 広告費: {row[‘広告費’]}万円, 気温: {row[‘気温’]}℃, “
          f”週末: {‘はい’ if row[‘週末’]==1 else ‘いいえ’}”)
    print(f” → 予測売上: {predictions[i]:.2f}万円”)
　

以下が出力になります。

　
=== 予測シナリオ ===

シナリオ1:
  広告費: 50万円, 気温: 25℃, 週末: いいえ
  → 予測売上: 247.50万円

シナリオ2:
  広告費: 80万円, 気温: 25℃, 週末: いいえ
  → 予測売上: 322.24万円

シナリオ3:
  広告費: 50万円, 気温: 30℃, 週末: はい
  → 予測売上: 296.64万円
　

✎コラム：数字の「正解」よりも、現場の「納得感」を

データの関係性を数式にする「回帰分析」。Pythonを使えば一瞬で答えが出ますが、私たち分析屋が大切にしているのは、その数字が「現場の実感と合っているか」です。

たとえば、広告費と売上の関係を分析したとき、計算上の予測値がどんなに正確でも、現場の担当者が「この時期の売上は気温の影響も大きいはずだ」と感じていれば、その分析はまだ未完成です。

私たちは、計算機が出した「合理」に、現場の経験という「情理」を掛け合わせ、お客様が自信を持って次の一歩を踏み出せる「おもてなし分析」を追求しています。

結果をどう読むか

予測モデルを作成した後、モデルの性能と結果の2つを解釈する必要があります。

その際、統計的な数字とビジネス的な意味の両方を理解する必要があります。

1. R²（決定係数）を見る（性能評価）

R²は「モデルの予測精度」を示す指標（0.0〜1.0）です。

学術的に明確な指標の解釈はありませんが、概ね以下のような評価をします。

0.7以上：良いモデル（実用可能）
0.5〜0.7：まずまず（改善の余地あり）
0.5未満：精度が低い（変数の見直しが必要）

2. 残差プロットで診断する（性能評価）

残差（実測値 – 予測値）をプロットすることで、モデルの問題を発見できます。

良いモデルの条件：

残差が0の周りにランダムに散らばっている
予測値の大小に関わらず、残差の幅が一定

悪いモデルの兆候：

残差に曲線のパターンが見える → 非線形関係の可能性

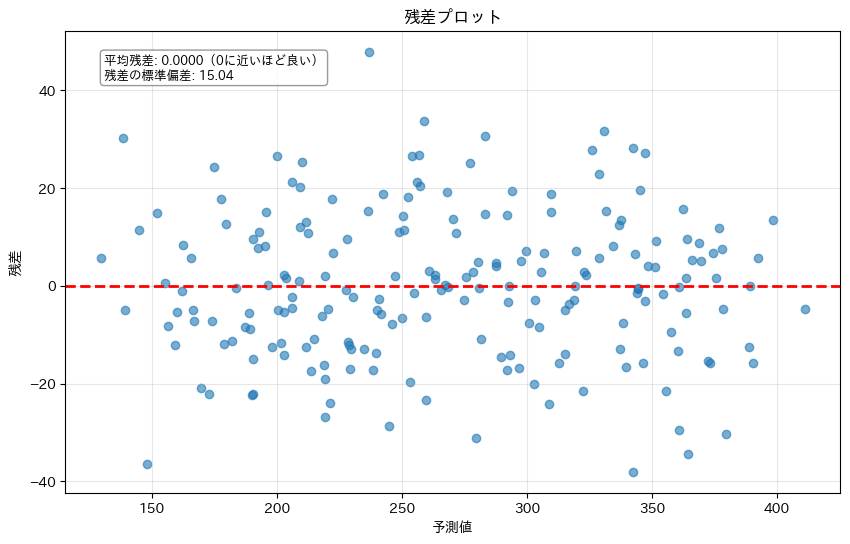
3. 回帰係数を見る（ビジネス的解釈）

回帰係数は「説明変数が1増えたとき、目的変数がどれだけ変化するか」を示します。

広告費の回帰係数 2.47：広告費を1万円増やすと、売上が約2.47万円増える
気温の回帰係数 2.88：気温が1度上がると、売上が約2.88万円増える
週末の回帰係数 36.75：平日より週末の方が約36.75万円売上が高い

また、予測というものにはどうしても誤差が生じてしまいます。

そのため、95%信頼区間も含めて回帰係数を評価することが大切です。

95%信頼区間とは「同じ手順で100回調査した場合、約95回はその範囲内に真の値が含まれる」という考えのものになります。

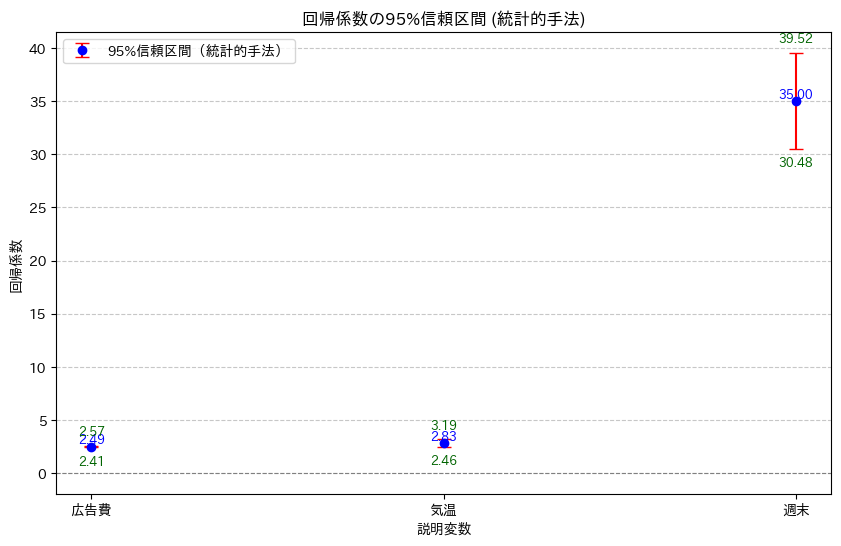
4. 統計的有意性 vs 実質的有意性（ビジネス的解釈）

統計的に意味があっても、ビジネス的に意味がないこともあります。

例：投資対効果（ROI）の計算

項目	金額	内容・計算根拠
広告費 (A)	10.00万円	投資額
売上増 (B)	24.91万円	A × ROAS
利益増 (C)	7.47万円	B × 利益率
純利益	-2.53万円	C – A
ROI	-25.3%	(純利益 ÷ A) × 100

重要：回帰係数が統計的に有意でも、ROIがマイナスなら実行すべきではありません。

この結果をもとに施策を考えるとしたら以下のようになります。

ROAS（広告運用効率）を上げる
クリエイティブの改善やターゲットの絞り込みを行い、10万円の広告費で33.4万円以上売れるようにする。

利益率を上げる
商品の単価を上げる、あるいは原価を抑え、利益率を40.2%以上に引き上げる。
（現在の売上24.91万円を維持する場合）

計算式：10万円 ÷ 24.91万円 = 40.14…%

LTV（リピート）で考える
「初回購入」だけで見るとROIはマイナスですが、その顧客が将来的に何度も購入してくれるのであれば、2回目以降は広告費がかからないため、中長期的にROIはプラスになります。

これらの施策候補から実行する施策を選出するため、さらなるデータ分析を行うのがデータサイエンティストの大事な仕事です。

✎コラム：R²（決定係数）よりも大切なこと。

分析モデルの精度を示す「R²（決定係数）」。実務では0.7以上が目安とされますが、私たちは数字の高さだけで一喜一憂しません。

統計的に正しくても、その施策を実行して「利益（ROI）」が出るかどうかは別問題だからです。広告費を増やして売上が上がっても、広告費以上に利益が削られては本末転倒ですよね。

データを「単なる予測」で終わらせず、具体的な「儲かる仕組み」や「守るべきコスト」というビジネスの言葉に翻訳すること。それが、分析屋が伴走支援で最も力を入れているポイントです。

よくある失敗と注意点

1. 相関と因果の混同

❌ 間違い：
「アイスの売上と溺死者数に相関がある → アイスを食べると溺死する」

✓ 正しい理解：
両方とも「気温」という第三の変数に影響されているだけ。

教訓：回帰分析は相関関係を示すが、因果関係を証明するものではない。

2. 学習範囲外での予測（外挿）

❌ 間違い：
「学習データが広告費10〜100万円の範囲なのに、200万円の場合を予測する」

✔ 正しい理解：
計算上は予測値が出るが、学習データにない領域のため数値は信頼できない。

教訓：モデルが学習した範囲内でのみ予測を使う。

3. 過学習

❌ 間違い：
「学習データに対して100%完璧に予測できるモデルが良いモデルだ」

✔ 正しい理解：
学習データに過剰に適合（特化）しすぎてしまい、未知のデータ（本番データ）では予測が当たらなくなる。

教訓：学習データへの精度だけでなく、未知のデータへの汎用性を重視する。

✎コラム：分析の「落とし穴」は、計算の外にある。

回帰分析でよくある失敗の一つに、データの範囲外を予測してしまう「外挿（がいそう）」があります。

広告費10万円〜100万円のデータで学習したモデルを使って、「じゃあ500万円投資したらどうなる？」と予測しても、その結果はあまり信頼できません。データが教えてくれるのは、あくまで「経験した範囲」のことだけだからです。

「データに何ができるか」と同じくらい「何ができないか」を正しく見極める。それが、ビジネスを読み間違えないためのデータサイエンティストの矜持です。

まとめ

回帰分析は、予測と要因分析のための基本的で強力なツールです。

この記事のポイント：

重回帰分析が実務では主流
Pythonなら数行で実装可能
R²と回帰係数でモデルを評価
統計的な有意性だけでなく、ROIなどビジネス的な意味も確認する
相関≠因果、範囲外の予測に注意

しっかり学びたい人へオススメする書籍

Pythonで学ぶあたらしい統計学の教科書第2版

https://www.shoeisha.co.jp/book/detail/9784798171944

効果検証入門～正しい比較のための因果推論／計量経済学の基礎

https://gihyo.jp/book/2020/978-4-297-11117-5

分析屋でデータサイエンティストのキャリアをスタートしよう

データサイエンティストには高度なデータ分析スキルに加え、ビジネス課題を解決へと導く力や、そこから新たな価値を見いだし、ビジネスアクションへとつなげる能力が求められます。現状では、必要とされるスキルをすべて兼ね備えていなかったとしても問題ありません。実務を通して知識やスキルを磨き、データサイエンティストへとステップアップしていくことは十分可能です。

分析屋では、「おもてなしの精神」を取り入れた育成環境のもと、単なるデータ分析にとどまらず、本質的な意思決定支援ができる人材を育成しています。技術力はもちろん、ビジネス理解や対話力も養えるため、データを活かす力を最大限に引き出せる環境が整っています。顧客の課題解決に寄り添いながら成長を目指すことで、市場価値の高いデータサイエンティストとしてのキャリアを築くことができるでしょう。

データをビジネス成果に結びつける、本物のデータサイエンティストを目指したい方は、ぜひ分析屋の採用ページをご覧ください。

➤採用サイトはこちら [分析屋採用サイトへ]